1、讨论未串接控制器时,闭环系统的输出是否达到性能指标要求。
在Matlab中对 $ G_{(s)}=\frac{12}{(s+1)(s+2)(s+3)} $ 进行仿真可得输出响应如下图所示: 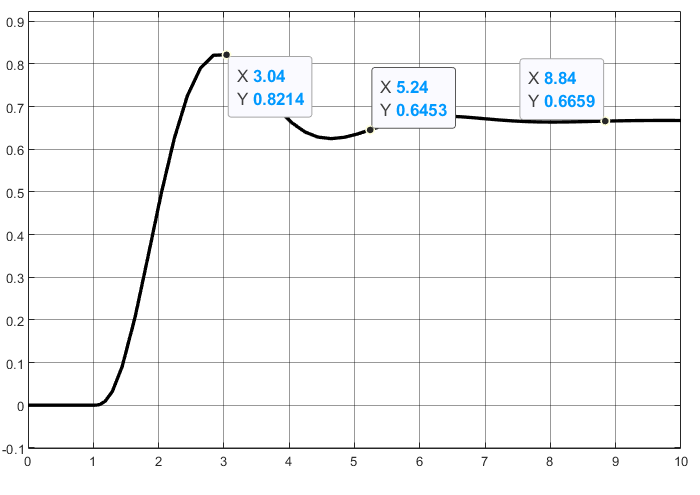 由图像可知,调节时间Ts=5.24s;超调量$\sigma \%=\frac{0.8214-0.6659}{0.6659} \times 100 \%=23.35 \%$,达不到性能指标要求。
由图像可知,调节时间Ts=5.24s;超调量$\sigma \%=\frac{0.8214-0.6659}{0.6659} \times 100 \%=23.35 \%$,达不到性能指标要求。
2、扩充临界比例度法
(1)、求出临界稳定时对应的K值。
运行代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
g=tf(num,den);
rlocus(g);求得根轨迹如下图所示: 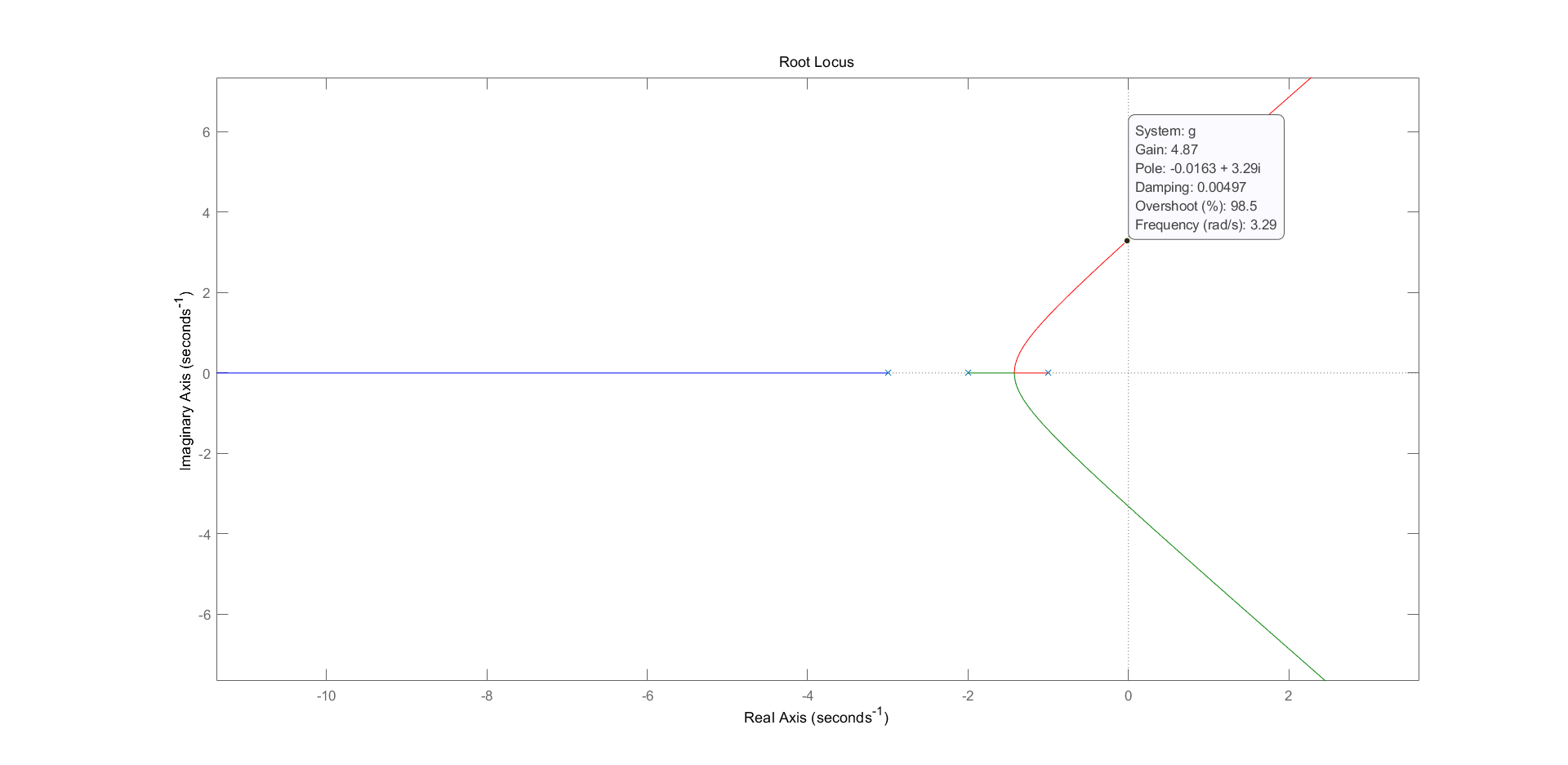 由图像可知,临界点对应的增益K=4.87。
由图像可知,临界点对应的增益K=4.87。
(2)、画出纯比例控制时的系统临界稳定输出图形,求出临界比例度和临界振荡周期。
运行代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
g=tf(num,den);
kp=4.87;
gc=feedback(g*kp,1);
t=0:0.01:10;step(gc,t);
grid on;求得临界稳定输出图形如下图所示: 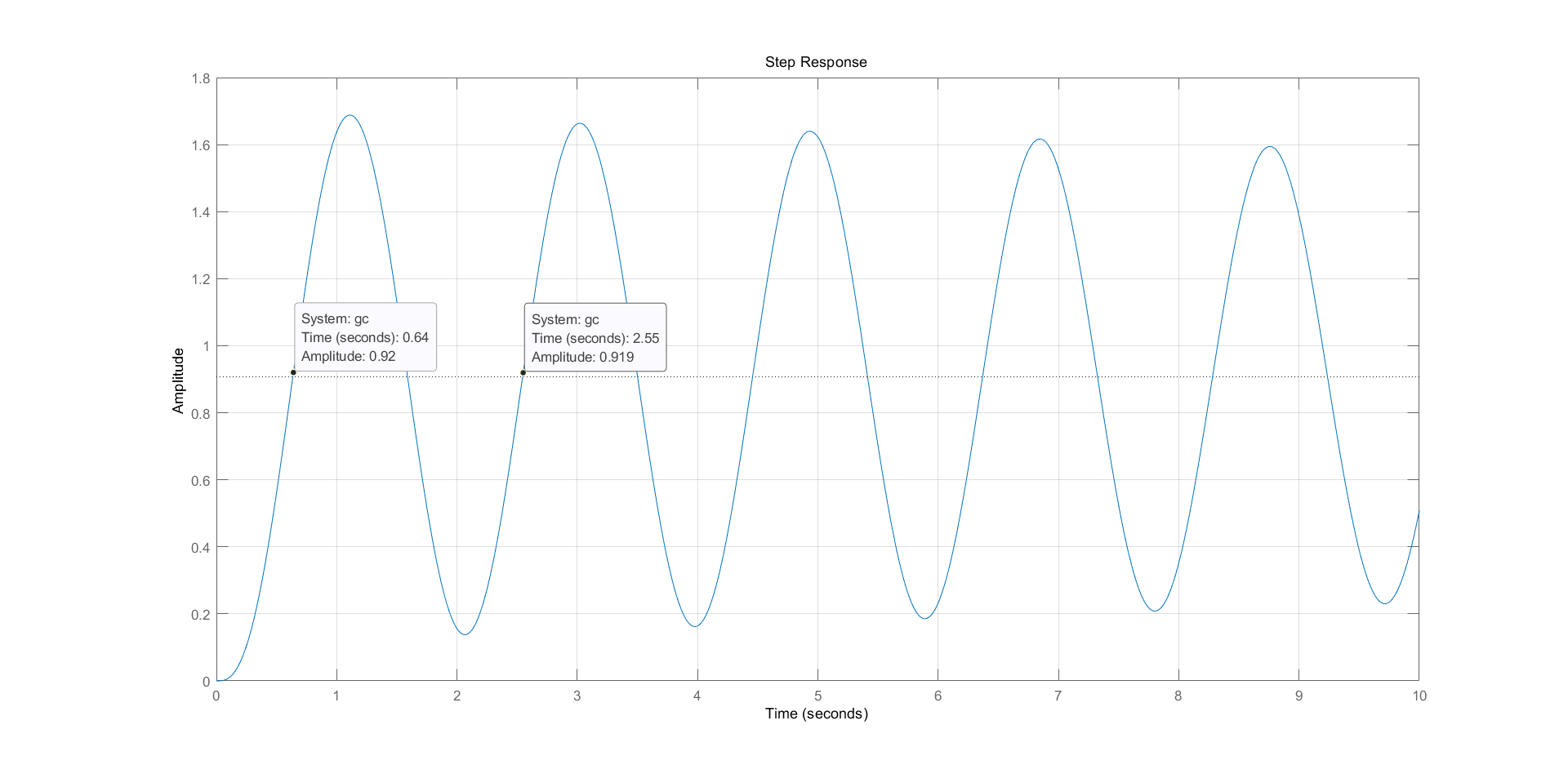 临界振荡周期Tr=1.91s;临界比例度为1/4.87。
临界振荡周期Tr=1.91s;临界比例度为1/4.87。
(3)、根据扩充临界比例度法,写出模拟调节器控制度为1.05和控制度为1.5时的系统的PID参数。
获取控制度为1.05的PID参数,运行以下代码:
tu=1.91;
detak=1/4.87;
T=0.014*tu;
kp=0.63*detak;
ti=0.49*tu;
td=0.14*tu;
T,kp,ti,td计算得PID参数为: 比例系数KP =0.1294,积分时间常数TI =0.9359,微分时间常数TD=0.2674,采样周期T=0.2674。 获取控制度为1.5的PID参数,运行以下代码:
tu=1.91;
detak=1/4.87;
T=0.09*tu;
kp=0.34*detak;
ti=0.43*tu;
td=0.20*tu;
T,kp,ti,td计算得控制度为1.5时的PID参数为: 比例系数KP =0.0698,积分时间常数TI =0.8213,微分时间常数TD=0.3820,采样周期T=0.1719。
(4)、根据扩充临界比例度法,写出控制度为1.05和控制度为1.5时的系统的位置式PID控制算式。
控制度为1.05时:$T=0.014 \operatorname{Tr}$ ; $\mathrm{Kp}=0.63 \delta{r} $; $T{I}=0.49 \operatorname{Tr} $; $T_{d}=0.14 \mathrm{Tr}$
控制度为1.5时:$T=0.09 \mathrm{Tr} $; $\mathrm{Kp}=0.34 \delta{r} $; $T{I}=0.43 \mathrm{Tr} $; $T_{d}=0.20 \mathrm{Tr}$
(5)、画出模拟调节器、控制度为1.05和控制度为1.5时的系统的单位阶跃响应图。讨论不同控制度的PID参数变化情况,分析控制效果(性能指标)。
运行下列代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
gg=tf(num,den);
t=0:0.01:10;
figure(1);
step(gg,'y');
hold on;
%以下用扩充临界比例度法进行参数整定¨
tu=1.91;
detak=1/4.87;
%控制度为1.05的PID控制器
T=0.014*tu;
kp=0.63*detak;
ti=0.49*tu;
td=0.14*tu;
ggd=c2d(gg,T,'zoh');
d0=1+T/ti+td/T;
d1=-1-2*td/T;
d2=td/T;
numd=kp*[d0 d1 d2];
dend=[1 -1 0];
dd=tf(numd,dend,T);
sysd=feedback(ggd*dd,1);
step(sysd,'r');
hold on;
%控制度为1.5的PID调节器
T=0.09*tu;
kp=0.34*detak;
ti=0.43*tu;
td=0.20*tu;
ggd=c2d(gg,T,'zoh');
d0=1+T/ti+td/T;
d1=-1-2*td/T;
d2=td/T;
numd=kp*[d0 d1 d2];
dend=[1 -1 0];
dd=tf(numd,dend,T);
sysd=feedback(ggd*dd,1);
step(sysd,'b');
title('黄线:未串接控制器的单位阶跃响应。红线:串接1.05的PID;蓝线:串接1.5的PID');获得未串接PID控制器、串接1.05PID控制器和串接1.5PID控制器的开环阶跃响应如下图所示: 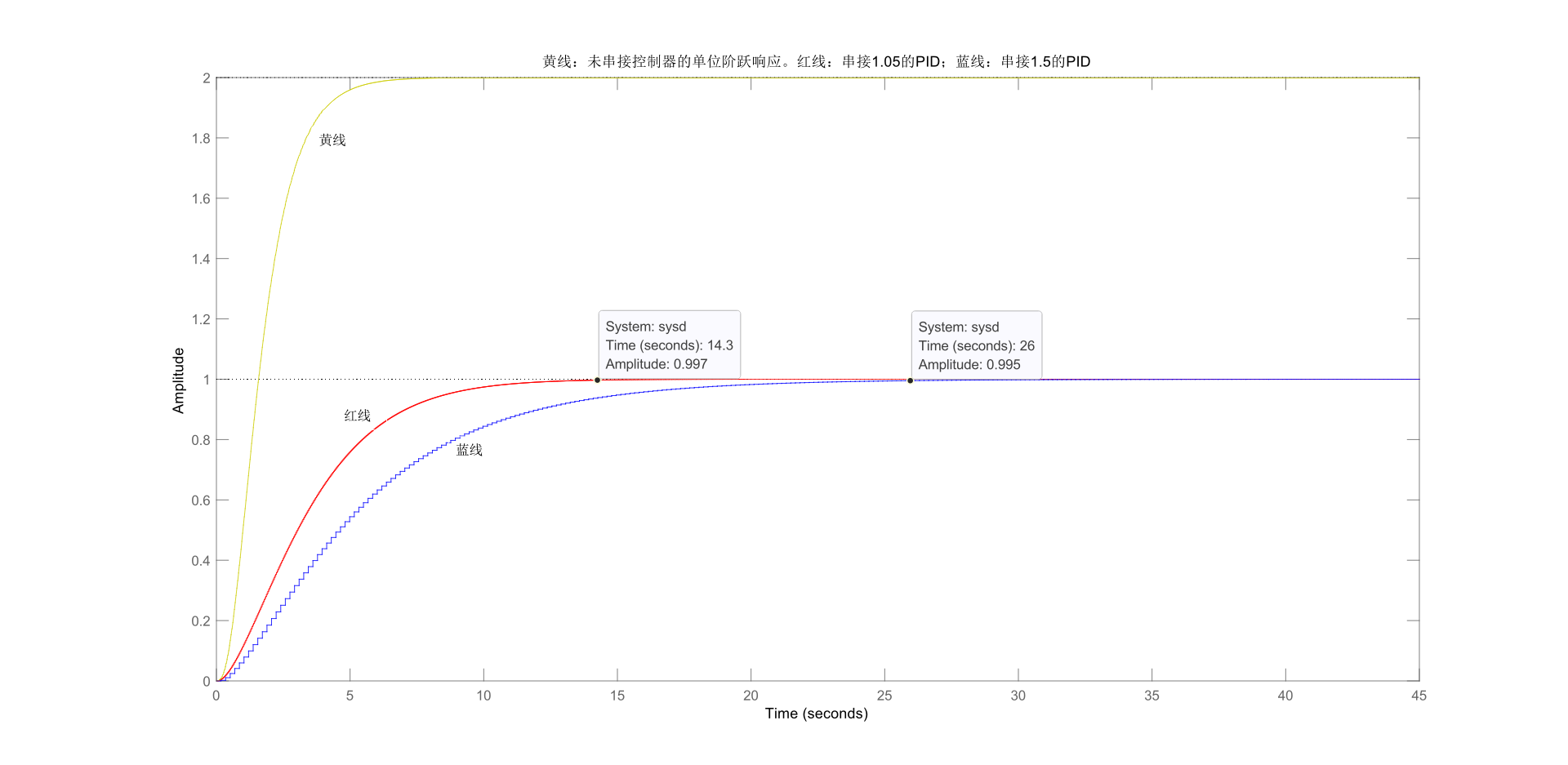 由图可看出,未串接PID控制器时,系统超调量100%。串接1.05控制度的PID控制器或1.5控制度的PID控制器后,系统无超调量。串接1.05控制度的PID控制器的系统上升时间为14.3s,串接1.05控制度的PID控制器的系统上升时间为26s。根据不同控制度的响应曲线,可知控制度为1.05的上升时间更小,更接近性能指标。
由图可看出,未串接PID控制器时,系统超调量100%。串接1.05控制度的PID控制器或1.5控制度的PID控制器后,系统无超调量。串接1.05控制度的PID控制器的系统上升时间为14.3s,串接1.05控制度的PID控制器的系统上升时间为26s。根据不同控制度的响应曲线,可知控制度为1.05的上升时间更小,更接近性能指标。
3、试凑法
选择扩充临界比例度法中控制度为1.05的PID参数,代入系统,根据试凑法调节系统PID参数中的T,Kp,Ti,Td的值,使系统输出满足给出的性能指标要求,给出满足指标要求的T,Kp,Ti,Td的值及单位阶跃响应图。 由于系统没有超调,要加快系统的响应,可增加kp的值,使比例项作用更快,增大积分系数,积分作用减弱,减小Kp增大后出现的超调量。所以在原来1.05的参数基础上增大kp和增大积分系数至输出达到性能指标要求。
运行下列代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
gg=tf(num,den);
tu=1.91;
detak=1/4.87;
%以控制度为1.05的PID参数为初值进行试凑
T=0.014*tu;
kp=1.8*detak; %增大kp
ti=0.65*tu; %增大ti
td=0.14*tu;
T,kp,ti,td
ggd=c2d(gg,T,'zoh');
d0=1+T/ti+td/T;
d1=-1-2*td/T;
d2=td/T;
numd=kp*[d0 d1 d2];
dend=[1 -1 0];
dd=tf(numd,dend,T);
sysd=feedback(ggd*dd,1);
t=0:0.01:10;
figure(2);
step(sysd,'b');
hold on;
%控制度为1.05的PID
kp=0.63*detak;
ti=0.49*tu;
td=0.14*tu;
T=0.014*tu;
ggd=c2d(gg,T,'zoh');
d0=1+T/ti+td/T;
d1=-1-2*td/T;
d2=td/T;
numd=kp*[d0 d1 d2];
dend=[1 -1 0];
dd=tf(numd,dend,T);
sysd=feedback(ggd*dd,1);
step(sysd,'r');
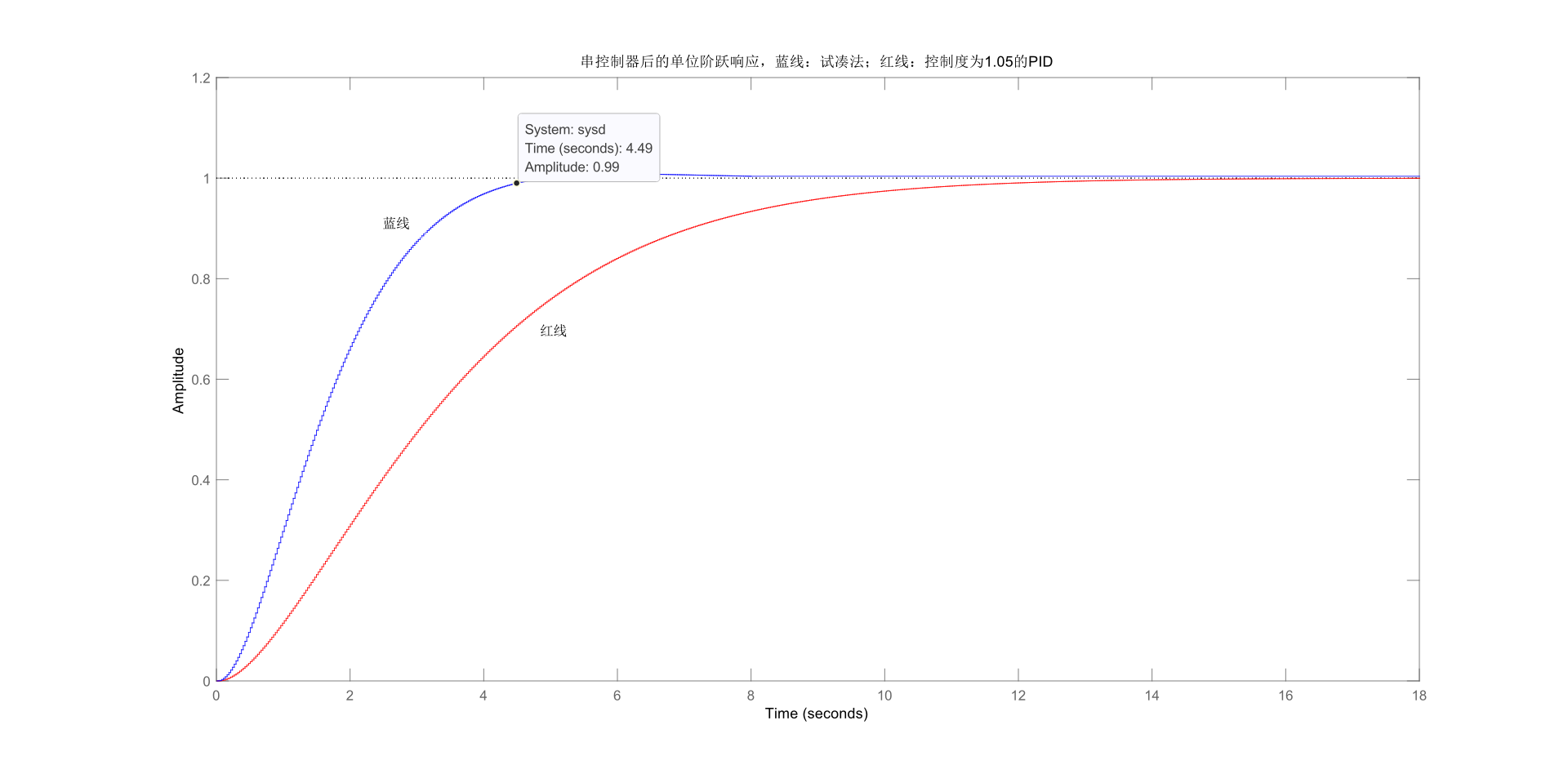
title('串控制器后的单位阶跃响应,蓝线:试凑法;红线:控制度为1.05的PID');试凑法得到的响应曲线,上升时间4.49s,无超调量,符合性能要求。 试凑法获得的PID参数:Kp=0.3696;Ti=1.2415;Td=0.2674;T=0.0267s
4、扩充响应曲线法
(1)、画出对象阶跃响应曲线图,求出等效滞后时间常数τ和等效惯性时间常数Tm。
运行下列代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
gg=tf(num,den);
step(gg);
k=dcgain(gg)计算得,K=2,对象阶跃响应曲线图如下所示: 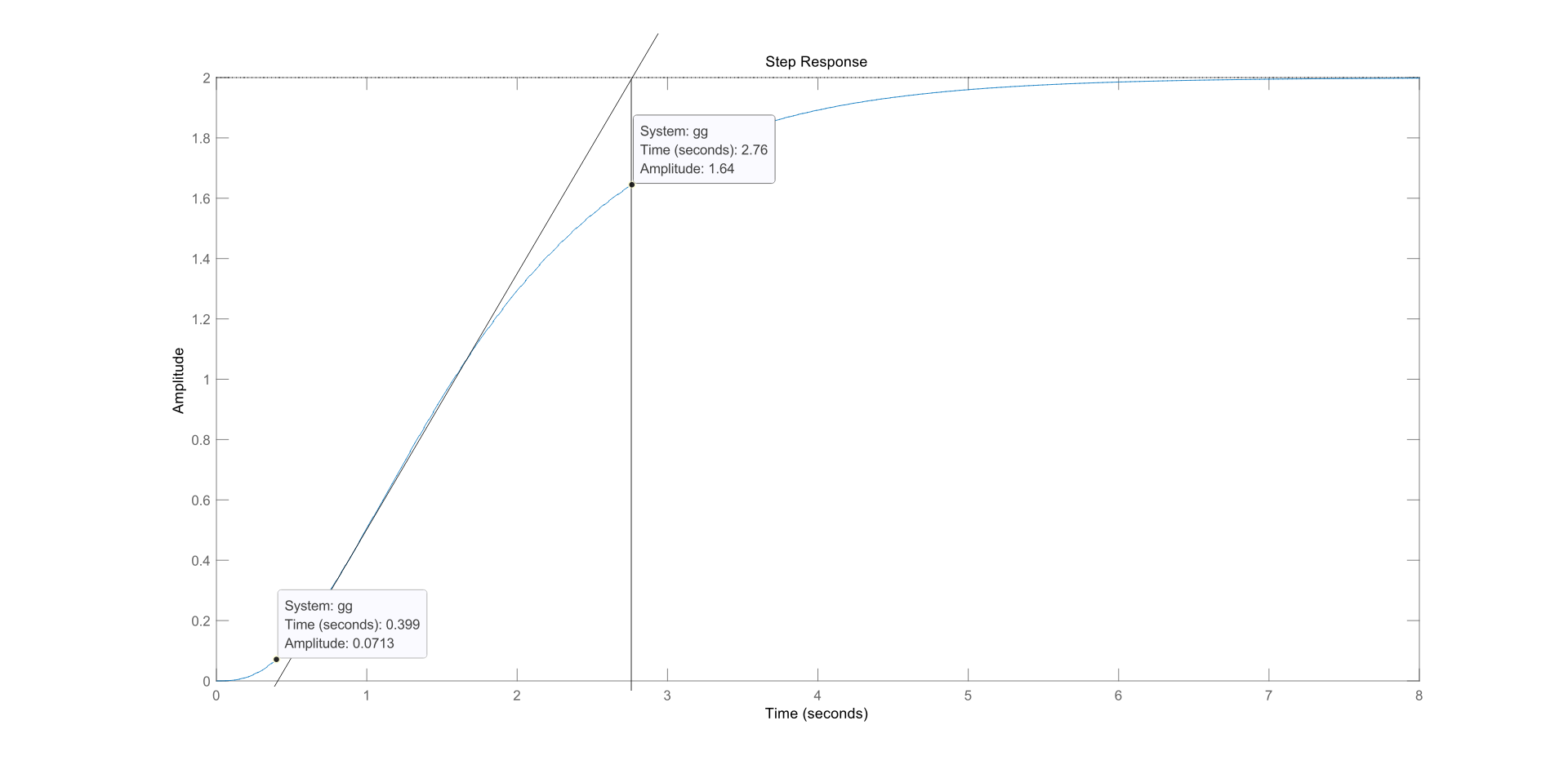 由图可知,τ=0.399;Tm=2.76-0.399=2.361
由图可知,τ=0.399;Tm=2.76-0.399=2.361
(2)、根据扩充响应曲线法,选取合适的控制度,写出对应的PID参数。
选取1.05控制度的PID控制器,运行下列代码:
num=12;
den=conv([1,1],conv([1,2],[1,3]));
gg=tf(num,den);
figure(1);
step(gg);
tao=0.399;
Tm=2.361;
%选取控制度为1.05
T=0.05*tao;
kp=0.15*Tm/tao;
ti=2*tao;
td=0.45*tao;
T,kp,ti,td,求得PID控制器参数:T = 0.0200;kp = 0.8876;ti = 0.7980;td = 0.1796。



Comments NOTHING